- Autors Matthew Elmers [email protected].
- Public 2024-01-11 08:52.
- Pēdējoreiz modificēts 2025-01-24 09:30.
Šajā rakstā mēs centīsimies izprast kaujas kuģu Bayern, Rivenge un Pensilvānijas šautenes bruņu iespiešanos, kā arī vācu, amerikāņu un britu bruņu salīdzinošo kvalitāti. To ir ārkārtīgi grūti izdarīt, jo dati par amerikāņu 356 mm, vācu 380 mm un britu 381 mm lielgabaliem ir ļoti ieskicēti un nepilnīgi, un dažreiz ir pretrunā viens otram, bet mēs tomēr centīsimies.
Kāda īsti ir problēma? Redzēsim, kā lielākā daļa jūras (un ne tikai) vēstures cienītāju salīdzina atsevišķu ieroču bruņu iespiešanos. Piemēram: vienā publikācijā, kas veltīta, piemēram, angļu dreadnoughts, ir informācija, ka Lielbritānijas Pirmā pasaules kara 381 mm šāviņš aptuveni 70 kabeļu attālumā iedūra 381 mm bruņu plāksni. Citā izdevumā, kas veltīts jau vācu "kapitāla" kuģiem - ka līdzīgs vācu 380 mm lādiņš "apguvis" 350 mm bruņas tikai ar 67, 5 kabeļiem. Šķiet, ka no tā izriet, ka angļu lielgabals ir jaudīgāks - tieši tāds secinājums izdarīts.
Tomēr patiesībā, šādi salīdzinot šādus datus, ir ļoti viegli iekļūt juceklī.
Vai iepriekš minētie dati ir iegūti reālas šaušanas rezultātā, vai arī tie tiek aprēķināti, izmantojot bruņu iespiešanās metodes? Ja šie ir faktiskās šaušanas rezultāti, vai abi ieroči bija identiski? Ja bruņu iespiešanās tika iegūta, aprēķinot, vai tad tika izmantotas tās pašas metodes? Vai iegūtie dati ir attiecīgo ministriju un departamentu speciālistu darba rezultāts, vai tie ir vēsturnieku aprēķinu rezultāts, kuri ir paņēmuši kalkulatoru? Skaidrs, ka otrajā gadījumā precizitāte būs daudz zemāka … Piemēri nav tālu jāmeklē: ņemsim slaveno S. Vinogradova monogrāfiju "Otrā reiha" Bayern "superdreadnoughts" un "Baden" ". Pielikumā Nr.2 cienījamais vēsturnieks kopā ar V. L. Kofmans veic daudz aprēķinu, lai salīdzinātu kaujas kuģu Rivenge un Bayern iespējas. Bet diemžēl pietiek ar 15 collu lielgabalu parametru tabulu (124. lpp.), Un mēs redzēsim, ka saskaņā ar cienījamu autoru aprēķiniem angļu 381 mm lielgabals ar pacelšanas leņķi 20, 25 grādiem ir tikai 105 kabeļu diapazons, tas ir, aptuveni 19, 5 tūkstoši m. Lai gan ārvalstu avoti vienādam sākotnējam ātrumam (732 m / s) un nedaudz zemākam pacēluma leņķim (20 grādi) sniedz ievērojami lielākus attālumus - 21, 3-21, 7 tūkstoši m. Protams, tomēr šādas novirzes no reālajām vērtībām visvairāk negatīvi ietekmē aprēķina rezultātus.
Bet pat tad, ja avoti uzrāda speciālistu aprēķinu rezultātus, par kuru precizitāti nav šaubu, rodas vēl viens faktors, kas sarežģī salīdzināšanu: šeit ir runa par bruņu kvalitāti. Skaidrs, ka tie paši briti, aprēķinot bruņu iespiešanos, veidojot konkrētu dredu, izmantoja atbilstošos britu bruņu rādītājus, vācieši - attiecīgi vācu utt. Un dažādu valstu bruņu izturība var atšķirties, taču tā joprojām ir puse no nepatikšanām: galu galā vienā valstī viena un tā pati Krupp bruņa tika pastāvīgi uzlabota. Tādējādi izrādās, ka artilērijas sistēmu aprēķini, kas veikti, piemēram, Anglijā, un acīmredzot vienām un tām pašām Krupp bruņām, bet veikti dažādos laikos, var izrādīties nesalīdzināmi. Un, ja mēs tam pievienojam gandrīz pilnīgu nopietna darba trūkumu bruņu korpusa attīstībā dažādās pasaules valstīs …
Kopumā vairāk vai mazāk ticams bruņu iespiešanās salīdzinājums nav tik vienkāršs uzdevums, kā varētu šķist no pirmā acu uzmetiena. Un draudzīgā veidā nespeciālistam (kurš, bez šaubām, ir šī raksta autors) labāk neņemties šo lietu. Bet, diemžēl - par dziļu nožēlu, profesionāļi kaut kā nesteidzas risināt šos jautājumus, tāpēc … kā saka, ja nav apzīmogota papīra, mēs rakstām vienkāršā tekstā.
Protams, iepriekšminēto artilērijas sistēmu pilna mēroga testus vairs nav iespējams veikt, tāpēc mūsu liktenis ir aprēķini. Un ja tā, tad ir jāpasaka vismaz pāris vārdi par bruņu iespiešanās formulām. Ja tiek publicētas mūsdienīgas aprēķina metodes, tad tikai slēgtos izdevumos un populārajā literatūrā parasti tiek dota Jēkaba de Māra formula. Interesanti, ka Jūras akadēmijas profesors L. G. Gončarovs savā 1932. gada artilērijas mācību grāmatā to nosauca par Jēkaba de Māra formulu. Šī formula kopā ar daudzām citām bija plaši izplatīta pagājušā gadsimta sākumā, un, jāsaka, tā ir diezgan precīza - iespējams, tā ir pat visprecīzākā starp šo gadu līdzīgajām formulām.
Tās īpatnība slēpjas faktā, ka tas nav fizisks, tas ir, tas nav fizisku procesu matemātisks apraksts. De Māra formula ir empīriska, tā atspoguļo dzelzs un tērauda-dzelzs bruņu eksperimentālās lobīšanas rezultātus. Neskatoties uz šo "nezinātnisko dabu", de Māra formula parādīja labāku tuvināšanos faktiskajiem šaušanas rezultātiem un uz Krupp bruņām nekā citas izplatītas formulas, un tāpēc mēs to izmantosim aprēķinos.
Interesenti šo formulu atradīs šī raksta pielikumā, taču nevajag piespiest visus, kas lasa šo materiālu, to saprast - tas nav nepieciešams, lai saprastu raksta secinājumus. Mēs tikai atzīmējam, ka aprēķinā tiek izmantoti ļoti vienkārši un pazīstami jēdzieni visiem tiem, kurus interesē militārās flotes vēsture. Tie ir šāviņa masa un kalibrs, bruņu biezums, šāviņa trieciena leņķis pret bruņām, kā arī šāviņa ātrums, kad tas atsitās pret bruņu plāksni. Tomēr de Mārs, protams, nevarēja aprobežoties ar iepriekš minētajiem parametriem. Galu galā šāviņa iespiešanās ir atkarīga ne tikai no tā kalibra un masas, bet arī zināmā mērā arī no formas un tērauda, no kura tas ir izgatavots, kvalitātes. Un bruņu plāksnes biezums, ko šāviņš spēj pārvarēt, protams, ir atkarīgs ne tikai no šāviņa darbības, bet arī no bruņu kvalitātes. Tāpēc de Mārs formulā ieviesa īpašu koeficientu, kas patiesībā ir paredzēts, lai ņemtu vērā norādītās bruņu un šāviņa īpašības. Šis koeficients palielinās, palielinoties bruņu kvalitātei, un samazinās, pasliktinoties šāviņa formai un kvalitātei.
Faktiski galvenās grūtības, salīdzinot dažādu valstu artilērijas sistēmas, ir tieši "balstītas" tieši uz šo koeficientu, ko mēs turpmāk vienkārši sauksim (K). Mums tas būs jāatrod katram no iepriekš minētajiem rīkiem - ja, protams, vēlamies iegūt nedaudz pareizu rezultātu.
Tātad, vispirms pieņemsim diezgan plaši izplatītus datus par bruņu iespiešanos vācu 380 mm / 45 lielgabalā "Bayern", saskaņā ar kuru lielgabals 12 500 m attālumā (tie paši 67, 5 kabeļi) varētu iekļūt 350 mm bruņas. Mēs izmantojam ballistisko kalkulatoru, lai atrastu 750 kg šāviņa parametrus, ar sākotnējo ātrumu 800 m / s trieciena brīdī uz bruņām: izrādās, ka šāds šāviņš trāpīs stingri vertikāli novietotā bruņu plāksnē plkst. leņķis 10, 39 grādi, ar ātrumu 505, 8 m / sek. Neliela atruna - turpmāk, runājot par šāviņa trieciena leņķi, mēs domājam tā saukto "leņķi no normas". "Normāls" ir tad, kad šāviņš triec bonneplītu stingri perpendikulāri tā virsmai, tas ir, 90 grādu leņķī. Attiecīgi šāviņš trāpīja 10 grādu leņķī.no parastā nozīmē, ka tas trāpīja pret plāksni 80 grādu leņķī. līdz tās virsmai, atkāpjoties no "atskaites" 90 grādiem. par 10 grādiem.
Bet atpakaļ pie vācu lielgabala bruņu iespiešanās. Koeficients (K) šajā gadījumā būs aptuveni (noapaļots līdz tuvākajam veselam skaitlim), kas vienāds ar 2083 - šī vērtība uzskatāma par diezgan normālu Pirmā pasaules kara laikmeta bruņām. Bet šeit rodas viena problēma: fakts ir tāds, ka datu avots par bruņu iekļūšanu ir grāmata "Otrā pasaules kara vācu kapitāla kuģi", kur Bayern 380 mm / 45 lielgabals tika salīdzināts ar kaujas kuģa galveno kalibru "Bismarks". Un vai nevarētu būt tā, ka aprēķinos tika ņemti vērā Krupp bruņu rādītāji, kas izveidoti intervālā starp diviem pasaules kariem, kas bija daudz spēcīgāks par to, kas tika uzstādīts Bayenne, Rivenge un Pennsylvania? Turklāt elektroniskā enciklopēdija navweaps ziņo, ka ir pierādījumi, ka 20 000 m attālumā vācu 380 mm apvalki spēja iekļūt 336 mm bruņu plāksnē, un mēs runājam par Pirmā pasaules kara laikmeta bruņām.
Nu, mēs uzskatām: pie 20 km krišanas leņķis būs 23,9 grādi, šāviņa ātrums uz bruņām ir 410,9 m / s, un koeficients (K) - daži nelaimīgie 1618, kas neietilpst bruņās. pretestības vērtības visos Pirmā pasaules kara laikmetos. Līdzīgs rezultāts parasti pietuvina Vācijā ražotās Krupp bruņas viendabīgai bruņu pretestībai … Acīmredzot navweaps dati satur kaut kādu kļūdu.
Mēģināsim izmantot citu informācijas avotu. Līdz šim mēs izmantojām aprēķinātos datus, un tagad mēģināsim tos salīdzināt ar Vācijas 380 mm / 45 lielgabala faktisko testu rezultātiem: tos ir norādījis S. Vinogradovs iepriekš minētajā vācu valodā veltītajā monogrāfijā. kaujas kuģi.
Tajā aprakstītas 3 šāvienu sekas ar bruņas caururbjošiem šāviņiem pret bruņu plāksnēm, kuru biezums ir 200, 290 un 450 mm, pēdējais mums ir visinteresantākais: 734 kg smags šāviņš trāpīja bruņu plāksnei 0 leņķī. (tas ir, 90 grādu leņķī pret virsmu) un ar ātrumu 551 m / s caur plāksni caurdurta 450 mm. Līdzīgs rezultāts atbilst koeficientam (K) 1 913, bet patiesībā tas būs nedaudz zemāks, jo vācieši atrada savu šāviņu pat 2 530 m aiz šķēršļa, kuru tas iedūra, un - kopumā. Diemžēl, ja nav datu par to, cik daudz šā attāluma šāviņš lidoja pa gaisu, cik - "brauca" pa zemi, ir absolūti neiespējami noteikt enerģiju, ko tā uzglabā pēc bruņu iekļūšanas.
Tagad ņemsim britu 381 mm / 42 artilērijas sistēmu. Diemžēl dati par tā bruņu iekļūšanu ir diezgan neskaidri: piemēram, V. L. Kofman, ir minēts fakts, ka šie britu ieroči caurdura bruņas, sava kalibra biezumā apmēram 70 kabeļu attālumā. Bet ar kādu šāviņu un ar kādu sākotnējo ātrumu? Ņemot vērā faktu, ka atsauce ir iekļauta kaujas kreiserim "Hood" veltītajā monogrāfijā un attiecas uz šī kuģa radīšanas periodu, var pieņemt, ka runa ir par 871 kg smagu čaulu. Tomēr šeit rodas vēl viens jautājums: šāda šāviņa oficiālais sākotnējais ātrums bija 752 m / s, bet daži britu aprēķini tika veikti ar mazāku ātrumu 732 m / s, tad kāda vērtība mums būtu jāņem? Tomēr neatkarīgi no tā, kādu ātrumu mēs izmantojam, koeficients (K) svārstīsies 1 983 - 2 048 robežās, un tas ir lielāks, nekā mēs aprēķinājām vācu lielgabala vērtībai (K). Var pieņemt, ka tas runā par britu bruņu kvalitātes pārākumu salīdzinājumā ar vācu … vai arī tas, ka vācu šāviņa ģeometriskā forma bija labāk piemērota iekļūšanai bruņās? Vai varbūt visa būtība ir tāda, ka V. L. Kofman ir aprēķinātas vērtības, bet vai praksē britu čaumalas sasniegtu labāku rezultātu?
Mūsu rīcībā ir dati par kaujas kuģa "Bādene" apšaudes rezultātiem

Tātad, viens no britu čaumalām, sitot 18 grādu leņķī. ar ātrumu 472 m / sek., "pārspēja" Vācijas galvenā kalibra torņa 350 mm frontālās bruņas. Šie dati ir vēl jo vērtīgāki, jo šajā gadījumā lobīšanai tika pakļautas nevis britu, bet vācu bruņas, tas ir, 381 mm / 42 un 380 mm / 45 lielgabalu testi ir vienā koordinātu sistēmā..
Ak, tie mums pārāk nepalīdz. Ja mēs pieņemam, ka angļu čaula caurdura vācu torni, kā saka, “ar pēdējo spēku”, un, ja būtu 351 mm bruņas, tas nebūtu izdevies, tad viņa (K) būtu vienāds ar 2021. Starp citu, ir interesanti, ka S. Vinogradovs norāda, ka britu šāviņš, kas iekļuva Vācijas torņa 350 mm frontālās bruņās, vēlāk netika atrasts, bet patiesībā ziņojumā ir teikts kas cits - tas eksplodēja, un apraksts par to, kur fragmenti lidoja tornī.
Protams, mums nav absolūta pamata uzskatīt, ka šī iespiešanās bija 381 mm šāviņa robeža vai pat tuvu tam. Bet tomēr, saskaņā ar dažām netiešām pazīmēm, var pieņemt, ka tas tā bija. Uz to “norāda” vēl viens trāpījums: britu 871 kg smags šāviņš, kas 11 grādu leņķī ietriecas 350 mm bārbekā, lai gan bruņās varēja izveidot caurumu ar 40 cm diametru, bet tas netika iekšā bārbekā. pati, plīstot bruņu pārvarēšanas procesā. Šajā gadījumā trāpījums notika gandrīz pašā bārbeketa centrā, tas ir, bruņu plāksnes izliekumā, ja tam bija kāda ietekme, tas bija minimums.
No visa iepriekš minētā var mēģināt izdarīt dažus secinājumus, taču pierādījumu bāzes trausluma dēļ tie, protams, būs ļoti minēti.
1. secinājums: Pirmā pasaules kara laikā vācu bruņas izturības ziņā aptuveni sakrita ar britiem. Šis secinājums ir spēkā, ja V. L. Kofmanam, ka britu 381 mm / 42 lielgabals bija spējīgs iekļūt bruņās, kas vienādas ar tā kalibru par 70 kbt, un, ja mēs nekļūdītos, pieņemot, ka 350 mm Vācijas torņa frontālās plāksnes iespiešanās 18 leņķī grādi un ātrums 472 m / s … ir britu 381 mm šāviņa iespiešanās robeža vai ļoti tuvu tai.
Secinājums 2. Acīmredzot vācu 380 mm šāviņa forma un kvalitāte nodrošināja labāku bruņu iespiešanos nekā angļu. Pamatojoties uz iepriekš minētajiem datiem, mēs varam pieņemt, ka britu 381 mm šāviņa koeficients (K), izšaujot uz vācu bruņām, bija aptuveni 2000, bet vācu 380 mm šāviņš bija aptuveni 1900. Ja mūsu pirmais ir pareizs, secinājums, ka Lielbritānijas un Vācijas bruņu pretestība bruņām ir aptuveni līdzvērtīga, ir acīmredzams, ka vienīgais zemākā koeficienta (K) iemesls var būt tikai pats šāviņš.
Kāpēc vācu apvalks varētu būt labāks? Tā kalibrs ir nedaudz mazāks, par vienu milimetru, bet, protams, tam diez vai varētu būt būtiska ietekme. Aprēķins rāda, ka ar tādu pašu masu (750 kg) kalibra maiņa par 1 milimetru palielinās bruņu iespiešanos par 1,03 milimetriem. Arī vācu šāviņš ir īsāks - tā garums bija 3,5 kalibrs, savukārt britu "Greenboy" garums ir 4 kalibrs. Iespējams, bija arī citas atšķirības. Protams, šeit liela nozīme ir tērauda kvalitātei, no kura tiek izgatavots šāviņš.
Tagad aprēķināsim vācu un britu ieroču bruņu iespiešanos 75 kabeļu attālumā - vispārpieņemts attālums izšķirošai cīņai, kur varēja sagaidīt pietiekami daudz triecienu, lai iznīcinātu līnijas ienaidnieka kuģi.
Norādītajā attālumā 871 kg britu 381 mm / 42 lielgabala šāviņa, kas tika izšauts ar sākotnējo ātrumu 752 m / s, trāpīja vertikāli novietotā bruņu plāksnē 13,05 grādu leņķī, bet tā ātrums-uz plāksnes. bija 479,6 m / s … Ar (K) vienāds ar 2000, saskaņā ar Džeikoba de Māra formulu, britu šāviņa bruņu iespiešanās bija 376, 2 mm.
Kas attiecas uz vācu apvalku, viss ir nedaudz sarežģītāk. Ja mūsu secinājums, ka bruņu iekļūšanas ziņā tas pārspēja angļu valodu, ir pareizs, tad vācu 380 mm / 45 lielgabala iespējas uz 75 kabeļiem bija ļoti tuvas angļu piecpadsmit collu lielgabalam. Šajā attālumā vācu 750 kg lādiņš trāpīja mērķim 12,42 grādu leņķī ar ātrumu 482,2 m / s, un pie (K), kas vienāds ar 1900, bruņu iespiešanās bija 368,9 mm. Bet, ja šī raksta autors joprojām maldās, un vācu pistolei ir vērts izmantot tādu pašu koeficientu kā angļu pistolei, tad 380 mm šāviņa iespējas samazinās līdz 342,9 mm.
Tomēr, pēc autora domām, vācu šāviņa bruņu iespiešanās ir vistuvāk 368, 9 mm (galu galā praktiskā šaušana deva koeficientu 1 913, neskatoties uz to, ka šāviņš lidoja tad 2,5 km), bet bruņu iespiešanās Angļu šāviņa aprēķins var būt nedaudz zemāks. Kopumā var uzskatīt, ka 75 kabeļu attālumā britu un vācu artilērijas sistēmas ir diezgan salīdzināmas bruņu iespiešanās ziņā.
Bet ar amerikāņu pistoli 356 mm / 45 viss izrādījās daudz interesantāks. Iepriekš minētie dati par čaumalām, kas sver 680 kg, krievu valodas literatūrā jāuzskata par kanoniskiem.
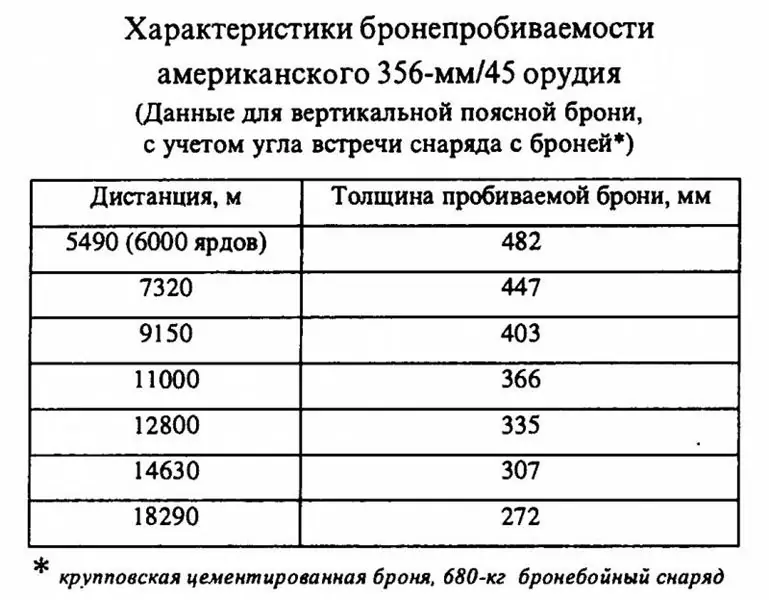
Faktiski šķiet, ka tajā norādītās vērtības liek izdarīt pilnīgi acīmredzamus secinājumus: ja pat 680 kg smagie čaumalas, kas parādījās Amerikas Savienotajās Valstīs pēc 1923. gada, ir zemākas par bruņu iespiešanos nekā to 380-381 mm Eiropas " kolēģi ", tad ko īsti runāt par agrākajiem 635 kg smagajiem šāviņiem, kas bija aprīkoti ar 356 mm amerikāņu dredu artilēriju! Tie ir vieglāki, kas nozīmē, ka lidojumā ātrāk zaudē ātrumu, savukārt to sākotnējais ātrums nepārsniedza smagākus apvalkus, un formas un kvalitātes ziņā 1923. gada munīcijai vajadzētu būt priekšrocībai. Ir skaidrs kā diena, ka amerikāņu "Pensilvānija", uzsākot ekspluatāciju, bruņu iekļūšanas ziņā bija zemāka par britu un vācu drediem. Nu, tas ir skaidrs, vai ne?
Tieši šādu secinājumu autors izdarīja, ņemot vērā amerikāņu četrpadsmit collu lielgabalu iespējas rakstā "Standarta" ASV, Vācijas un Anglijas kaujas kuģi. Amerikāņu "Pensilvānija" ". Un tad viņš paņēma kalkulatoru …
Fakts ir tāds, ka aprēķins pēc de Marra formulas parādīja, ka amerikāņu 356 mm / 45 lielgabaliem bija tabulā norādītā bruņu iespiešanās ar koeficientu (K), kas vienāds ar 2,317! Citiem vārdiem sakot, tabulā parādītie amerikāņu 680 kg lādiņi parādīja rezultātus, ja tika pakļauti bruņām, kas netika radītas Pirmā pasaules kara laikmetā, bet gan daudz vēlākos un izturīgākajos paraugos.
Grūti pateikt, cik lielā mērā bruņu aizsardzības spēks ir pieaudzis intervālā starp pirmo un otro pasaules karu. Krievu valodas avotos uz šo jautājumu ir tikai īsas un bieži vien pretrunīgas atsauces, uz kuru pamata var pieņemt, ka Kruppa bruņu spēks ir pieaudzis par aptuveni 20-25%. Tādējādi Pirmās pasaules laikmeta lielkalibra apvalkiem koeficienta (K) pieaugums būs no 1900 - 2000 līdz 2280 - 2500, taču šeit jāatceras, ka, palielinoties bruņu aizsardzības kvalitātei protams, palielinājās arī šāviņu kvalitāte, un tāpēc Otrā pasaules kara smagajai munīcijai (K) var būt mazāka. Tāpēc (K) 2 317 apmērā pēckara čaumalām, kas, protams, uzlabojās, ņemot vērā iepriekš gūto pieredzi, izskatās diezgan organiski, bet Otrā pasaules kara laikmeta bruņām, nevis pirmajām.
Bet, nosakot koeficientu (K) amerikāņu 680 kg čaumalām 2000 līmenī, tas ir, ienesot bruņu aizsardzības kvalitāti Pirmā pasaules kara laikmetā, 75 kabeļu attālumā mēs iegūsim bruņas iespiešanās 393,5 mm līmenī, tas ir, augstāka nekā britu un vācu piecpadsmit collu lielgabaliem!

Pārvēršana par 635 kg lādiņu dod ļoti nenozīmīgu korekciju - ballistiskais kalkulators parādīja, ka 75 kabeļu attālumā ar krišanas leņķi 10, 82 grādi. un ātrums "uz bruņām" 533, 2 m pie (K) vienāds ar 2000, amerikāņu šāviņš iekļūst Pirmā pasaules kara laikmeta bruņās, 380 mm biezs, tas ir, ievērojami vairāk nekā paša kalibrs!
No otras puses, ir pilnīgi iespējams, ka šāds aprēķins joprojām nav pilnīgi pareizs. Fakts ir tāds, ka saskaņā ar dažiem ziņojumiem koeficients (K) vienām un tām pašām bruņām samazinās, palielinoties šāviņa kalibram. Tā, piemēram, mūsu aprēķinos Vācijas 380 mm / 45 artilērijas sistēmas maksimālā vērtība (K), kas iegūta aprēķinos un publicēta avotos, ir 2083. Tajā pašā laikā aprēķini Vācijas 305 mm / 50 ieroči, kas tika uzstādīti uz Kaiserlichmarine kuģiem, sākot ar Heligolands, dati no avotiem par bruņu iespiešanos dod (K) 2145 līmenī. Attiecīgi ir iespējams, ka 356 mm / 45 lielgabali (K) = 2000 mēs izmantojām, lai aprēķinātu bruņu iekļūšanu amerikāņu ieročos joprojām ir pārāk mazs.
Turklāt diemžēl autoram nav nekādu "pavedienu", lai salīdzinātu amerikāņu Krupp bruņu bruņu pretestību ar Eiropas kolēģiem. Neatliek nekas cits, kā uzskatīt to par līdzvērtīgu vācu un angļu bruņu aizsardzībai, lai gan tas, protams, var nebūt.
Apkoposim visus šos diezgan haotiskos datus. Ņemot vērā aprēķinos izmantoto "metožu" kļūdas, ar lielu varbūtības pakāpi var pieņemt, ka Kaujas kuģu Rivenge, Bayern un Pennsylvania galveno kalibra lielgabalu vertikālās bruņu aizsardzības bruņu iespiešanās 75 kabeļu attālumā bija aptuveni vienāda un bija aptuveni 365-380 mm.
Neskatoties uz daudziem pieņēmumiem, mūsu rīcībā esošie dati joprojām ļauj izdarīt dažus secinājumus par vertikālo bruņu aizsardzību. Bet, izlaužot horizontālās barjeras, kas ir bruņu klāji, viss ir daudz sarežģītāk. Fakts ir tāds, ka Džeikobs de Mārs diemžēl nemaz neuztraucās, lai izveidotu formulu horizontālās aizsardzības spēka noteikšanai. Tās pamatformula, kas pielāgota mūsdienu bruņu veidiem, ir piemērota tikai cementētu bruņu aprēķināšanai, kuru biezums pārsniedz 75 mm. Šī formula ir dota šī raksta pielikumā Nr. 1, un visi iepriekšējie aprēķini rakstā tika veikti, izmantojot to.
Bet šo gadu kuģu klāji tika aizsargāti nevis ar cementētu (neviendabīgu), bet ar viendabīgām bruņām, kurām nebija virsmas sacietējuša slāņa. Šādām bruņām (bet - uzstādītas vertikāli!), Tiek izmantota cita formula, kas paredzēta, lai novērtētu necementētas bruņu plāksnes, kuru biezums ir mazāks par 75 mm, tā ir dota pielikumā Nr.
Vēlos atzīmēt, ka abas šīs formulas ir ņemtas no vairāk nekā nopietna avota: “Jūras taktikas gaita. Artilērija un bruņas 1932, autors - RKKA Jūras akadēmijas profesors L. G. Gončarovs, viens no vadošajiem ekspertiem pirmskara PSRS jūras artilērijas jomā.
Un diemžēl neviens no tiem nav piemērots horizontālās aizsardzības izturības novērtēšanai. Ja mēs izmantojam formulu cementētām bruņām, tad 75 kabeļu attālumā mēs iegūstam ierobežotu bruņu iespiešanos: 46,6 mm 381 mm / 42 britu, 39,5 mm 380 mm / 45 vācu un 33,8 mm 356 mm / 45 amerikāņu ieroči. Ja mēs izmantojam otro formulu necementētām bruņām, tad mēs iegūstam, ka, trāpot leņķī, kas raksturīgs 75 kabeļu attālumam, visas trīs artilērijas sistēmas viegli iekļūst 74 mm bruņu plāksnē, pēc tam saglabājot milzīgu kinētiskās enerģijas piedāvājumu - piemēram, angļu 381 mm, šāviņam, kas 75 mm kabeļu attālumā var iekļūt šāda biezuma bruņās, būs ātrums 264,5 m / s, bet tā ātrums būs 482,2 m / s. Ja mēs ignorējam bruņu plāksnes biezuma ierobežojumu, izrādās, ka britu 381 mm šāviņš saskaņā ar iepriekš minēto formulu spēj iekļūt klāja bruņās, kuru biezums pārsniedz 180 mm! Kas, protams, ir pilnīgi neiespējami.
Ja mēs mēģinām atsaukties uz Bayern klases kaujas kuģa testa rezultātiem, mēs redzēsim, ka bruņas caurdurošie 871 kg smagi britu čaumalas divreiz trāpīja torņu horizontālajās bruņās, kuru biezums bija 100 mm 11 grādu leņķī., kas atbilst 67,5 kabeļu attālumam šāviņam ar sākotnējo ātrumu 752 m / s un 65 kabeļiem - šāviņam ar sākotnējo ātrumu 732 m / s. Abas reizes bruņas netika caurdurtas. Bet vienā gadījumā lādiņš, rikošetējot, bruņās izveidoja gropi ar 70 cm dziļumu, tas ir, plāksne bija ļoti stipri saliekta. Un otrajā, lai gan apvalks atkal bija rikošets, bruņas bija ne tikai ieliektas par 10 cm, bet arī saplēstas.

Līdzīgais bojājumu raksturs liek domāt, ka, lai gan vācu 100 mm bruņas nodrošināja aizsardzību norādītajos attālumos, tas bija, ja ne pie iespējamās robežas, tad ļoti tuvu tam. Bet aprēķins pēc cementētās bruņas formulas dod bruņu iespiešanos tikai 46,6 mm lielā attālumā, kur krišanas leņķis būs lielāks, un attiecīgi lādiņam būtu vieglāk iekļūt klāja bruņās. Tas ir, pēc formulas izrādās, ka 100 mm klājam vajadzēja jokojot un ar lielu drošības rezervi atspoguļot angļu čaumalas - tomēr prakse to neapstiprina. Tajā pašā laikā, saskaņā ar aprēķiniem, izmantojot necementu bruņu formulu, izrādās, ka Bādenes galvenā kalibra jumtiem vajadzēja būt viegli caurdurtiem un - ar lielu čaulas enerģijas piegādi -, kas atkal nav vispār apstiprina prakse.
Man jāsaka, ka šādām aprēķinu neprecizitātēm ir pilnīgi loģisks izskaidrojums. Kā jau teicām iepriekš, de Māra formulas nav fizisku procesu matemātisks apraksts, bet ir tikai to modeļu fiksācija, kas iegūti, pārbaudot bruņas. Bet tika pārbaudīta vertikālā bruņu aizsardzība, nevis horizontāla, un nav pārsteidzoši, ka modeļi šajā gadījumā vienkārši pārstāj darboties: horizontāli novietotām bruņām, kurās čaumalas ietriecas ļoti nelielā leņķī pret to virsmu, šie raksti, protams, ir pilnīgi atšķirīgi.
Šī raksta autore "internetā" saskārās ar viedokļiem, ka de Māra formulas efektīvi darbojas pie novirzes leņķiem no normas ne vairāk kā 60 grādi, tas ir, no 30 grādiem līdz plāksnes virsmai un vairāk. Var pieņemt, ka šis novērtējums ir ļoti tuvu patiesībai.
Tādējādi mums ar nožēlu jāatzīst, ka autoram pieejamais matemātiskais aparāts neļauj veikt nekādus ticamus kaujas kuģu Rivenge, Bayern un Pennsylvania horizontālās aizsardzības pretestības aprēķinus. Ņemot vērā iepriekš teikto, būs grūti izmantot dažādos avotos sniegtos datus par horizontālo bruņu bruņu iespiešanos - parasti tie visi ir balstīti uz vieniem un tiem pašiem aprēķiniem pēc de Māra formulām un ir nepareizi.






