- Autors Matthew Elmers elmers@military-review.com.
- Public 2023-12-16 22:23.
- Pēdējoreiz modificēts 2025-01-24 09:30.

Kas nosaka precizitāti - viena no ieroča galvenajām īpašībām? Acīmredzot, no mucas un kārtridža kvalitātes. Pagaidām atliksim kasetni, bet ņemsim vērā procesa fiziku.
Paņemiet metāla stieni vai cauruli, kas izgatavota no elastīga metāla, un stingri nostipriniet to masīvā pamatnē. Tātad mēs iegūstam pētāmās ierīces modeli. Tagad, ja mēs atsitīsimies pret stieni, nav nozīmes, kurā vietā un kādā virzienā, vai nu velciet to atpakaļ, vai saspiediet, vai, visbeidzot, ievietojot kārtridžu mēģenē un izdarot šāvienu, mēs redzēsim, ka stienis (muca) ir nonākusi slāpētā svārstīgā kustībā. Šīs vibrācijas tiek sadalītas vienkāršākajās, un katrs šādas vienkāršas mucas vibrācijas veids savā veidā ietekmēs šaušanas precizitāti (precizitāti).
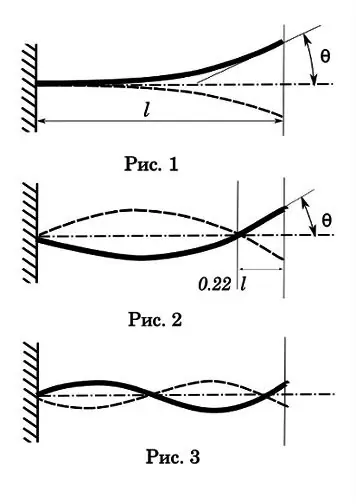
Sāksim ar pirmās kārtas vai piķa vibrācijām. Kā redzat (1. att.), Šādai svārstībai piestiprināšanas vietā ir tikai viens mezgls, lielākā amplitūda, garākais sabrukšanas laiks un garākais svārstību laiks vienā periodā. Šis laiks ir 0,017-0,033 sek. Ložu pārvietošanās laiks caur urbumu ir 0, 001-0, 002 sek. Tas ir, ievērojami mazāk nekā vienas svārstību cikls, kas nozīmē, ka šāda veida svārstībām nav būtiskas ietekmes uz viena šāviena precizitāti. Bet ar automātisku fotografēšanu var izrādīties interesants attēls. Pieņemsim, ka uguns ātrums ir 1200 rds / min, t.i. viena cikla laiks - 0,05 sek. Ar pirmās kārtas svārstību periodu 0, 025 sek, mums ir daudzkārtēja frekvenču attiecība. Un tas ir neaizstājams nosacījums rezonansei ar visām no tā izrietošajām sekām - ierocis sāk trīcēt ar tādu spēku, ka var sabrukt.
Pāriesim pie otrās kārtas svārstībām (2. att.). Bet es iesaku humanitāro zinātņu studentiem vispirms veikt eksperimentu, lai novērstu izglītības trūkumus fizikas jomā. Jums jāņem mazs zēns (jūs varat meitene), ielieciet viņu šūpolēs un šūpolēs. Pirms jums ir svārsts. Nostājieties šūpoles malā un mēģiniet trāpīt zēnam ar bumbu. Pēc virknes mēģinājumu jūs nonāksit pie secinājuma, ka labākais veids, kā trāpīt, ir tad, kad mērķis atrodas svārstību pirmajā fāzē - maksimālā novirze no līdzsvara punkta. Šajā brīdī mērķim ir nulles ātrums.
Apskatīsim otrās kārtas diagrammu. Otrais vibrācijas mezgls atrodas aptuveni 0,22 attālumā no mucas gala. Šis punkts ir dabas likums, nav iespējams radīt tādas vibrācijas konsoles staram, lai otrais mezgls nokristu uz brīvā gala. Tā ir vieta, kur tā atrodas, un nav atkarīga no mucas garuma.
Svārstību amplitūda otrās kārtas shēmai ir mazāka, bet svārstību laiks jau ir salīdzināms ar laiku, kad lode iet caur urbumu-0, 0025-0, 005 sek. Tātad atsevišķai fotografēšanai tas jau interesē. Lai būtu skaidrs, par ko mēs runājam, iedomājieties 1 metru garu mucu. Lode pārvietojas pa visu stobru 0, 001 sekundē. Ja svārstību periods ir 0,004 sek., Tad līdz brīdim, kad lode iziet no mucas, stobrs sasniegs maksimālo līkumu pirmajā fāzē. Humanitāro zinātņu jautājums ir - kurā brīdī (kurā fāzē) vislabāk ir izšaut lodi no mucas, lai nodrošinātu rezultātu konsekvenci? Atcerieties šūpoles. Nulles punktā stumbra novirzes ātruma vektors ir maksimāls. Lodei ir grūtāk trāpīt uz mucas griezuma šo punktu, tai ir arī sava kļūda ātrumā. Tas ir, labākais brīdis, kad lode izlidos, būs tad, kad muca atradīsies pirmās novirzes fāzes augstākajā punktā - kā attēlā. Tad nenozīmīgas lodes ātruma novirzes kompensēs ilgāks laiks, ko muca pavadīs visstabilākajā fāzē.
Diagrammā ir skaidri redzams šīs parādības grafisks attēlojums (4-5. Att.). Šeit - Δt ir laika kļūda, ar kuru lode šķērso mucas purnu. Att. 4 ir ideāls, ja vidējais lodes pacelšanās laiks sakrīt ar stobra svārstību nulles fāzi. (Matemātiķi! Es zinu, ka ātruma sadalījums ir nelineārs.) Apēnotā zona ir trajektoriju izplatīšanās leņķis.
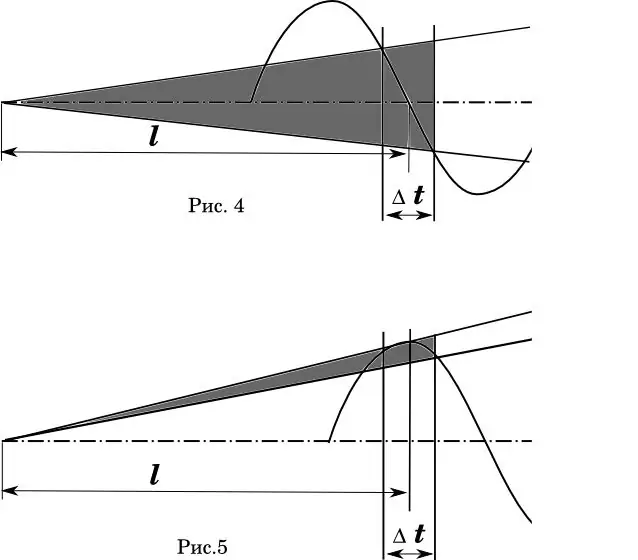
5. attēlā stobra garuma un ātruma kļūda paliek nemainīga. Bet mucas lieces fāze tiek pārvietota tā, lai vidējais izlidošanas laiks sakristu ar mucas maksimālo novirzi. Vai komentāri ir lieki?
Nu, vai tas ir sveces vērts? Cik nopietnas var būt novirzes, ko izraisa otrās kārtas svārstības? Nopietni un ļoti nopietni. Pēc padomju profesora Dmitrija Aleksandroviča Ventela teiktā, vienā no eksperimentiem tika iegūti šādi rezultāti: vidējās novirzes rādiuss palielinājās par 40%, stobra garumam mainoties tikai par 100 mm. Salīdzinājumam-augstas kvalitātes mucas apstrāde var uzlabot precizitāti tikai par 20%!
Tagad apskatīsim vibrācijas frekvences formulu:
kur:
k - koeficients otrās kārtas svārstībām - 4, 7;
L ir mucas garums;
E ir elastības modulis;
Es esmu sekcijas inerces moments;
m ir stumbra masa.
… un turpiniet analīzi un secinājumus.
Acīmredzamais secinājums no 4-5. Attēla ir lodes ātruma kļūda. Tas ir atkarīgs no pulvera kvalitātes un tā svara un blīvuma kārtridžā. Ja šī kļūda ir vismaz ceturtā daļa no cikla laika, tad no visa pārējā var atteikties. Par laimi, zinātne un rūpniecība šajā jautājumā ir sasniegusi ļoti lielu stabilitāti. Un sarežģītākām (piemēram, stendā) ir visi nosacījumi patronu salikšanai, lai lodes izlaišanas fāzi pielāgotu tieši stobra garumam.
Tātad, mums ir kasetne ar viszemāko iespējamo ātruma variāciju. Mucas garums tika aprēķināts, pamatojoties uz tā maksimālo svaru. Rodas jautājums par stabilitāti. Mēs skatāmies uz formulu. Kādi mainīgie ietekmē svārstību frekvences izmaiņas? Mucas garums, elastības modulis un masa. Šaušanas laikā muca sakarst. Var siltums mainīt mucas garumu, lai tiktu ietekmēta precizitāte. Jā un nē. Jā, tā kā šis skaitlis ir simtdaļas no procentiem 200 ° C temperatūrā. Nē, tā kā tērauda elastības moduļa izmaiņas tajā pašā temperatūrā ir aptuveni 8-9%, 600 ° C tas ir gandrīz divas reizes. Tas ir, daudzas reizes augstāks! Muca kļūst mīkstāka, mucas lieces fāze virzās uz priekšu līdz brīdim, kad aizzīme aiziet, precizitāte samazinās. Nu, ko saka pārdomāts analītiķis? Viņš teiks, ka nav iespējams iegūt maksimālu precizitāti vienā mucas garumā aukstā un karstā režīmā! Ieročam var būt labāka veiktspēja ar aukstu vai karstu stobru. Attiecīgi tiek iegūtas divu veidu ieroči. Viens ir par slazdošanas darbībām, kad mērķis jāsit no pirmā - "aukstā" šāviena, jo otrā precizitāte būs sliktāka mucas neizbēgamas sasilšanas dēļ. Šādā ieročā nav steidzami nepieciešama automatizācija. Un otrā klase ir automātiskās šautenes, kuru stobra garums ir pielāgots karstajam stobrim. Šajā gadījumā iespējamo izlaidumu zemās aukstā šāviena precizitātes dēļ var kompensēt ar ātru sekojošu karstu un precīzāku šāvienu.
EF Dragunovs ļoti labi zināja šī procesa fiziku, veidojot savu šauteni. Es iesaku jums iepazīties ar viņa dēla Alekseja stāstu. Bet vispirms kādam būs jālauž smadzenes. Kā zināms, konkursa finālam par snaipera šauteni tuvojās divi Konstantinova un Dragunova paraugi. Dizaineri bija draugi un palīdzēja viens otram it visā. Tātad, Konstantinova šautene tika "noregulēta" aukstā režīmā, Dragunova šautene uz "karsto". Cenšoties uzlabot sāncenša šautenes precizitāti, Dragunovs ar lielām pauzēm izšauj savu šauteni.

Apskatīsim formulu vēlreiz. Kā redzat, frekvence ir atkarīga arī no mucas masas. Stumbra masa ir nemainīga. Bet smags kontakts ar priekšgalu rada neprognozējamu pozitīvu atgriezenisko saiti uz mucu. Sistēmai-mucas priekšējai rokai (atbalstam) būs atšķirīgs inerces moments (masu kopums attiecībā pret piestiprināšanas punktu), kas nozīmē, ka tas var izraisīt arī fāzes nobīdi. Tāpēc sportisti izmanto mīkstu atbalstu. Tāda pati iezīme ir saistīta ar "piekārtā stobra" principa piemērošanu, kad ieroča priekšpusei nav stingra kontakta ar stobru un tas ir stingri piestiprināts pie tā (ieroča) tikai apvidū. uztvērēju, un otrs gals vai nu nepieskaras stobram, vai pieskaras caur atsperes savienojumu (SVD).
Galīgā doma. Fakts, ka ar tādu pašu mucas garumu nav iespējams iegūt vienādu precizitāti dažādās temperatūrās, ir lielisks iemesls, lai izstieptu smadzenes. Mucas garums un / vai masa ir jāmaina tikai tad, kad mainās mucas temperatūra. Nemainot mucas garumu vai svaru. No humanitāro zinātņu viedokļa tas ir paradokss. No tehniķa viedokļa ideāls uzdevums. Visa dizainera dzīve ir saistīta ar šādu problēmu risināšanu. Šerloki atpūšas.






